A coupon or coupon payment is the annual interest rate paid on a bond, expressed as a percentage of the face value and paid from the issue date until maturity.
Coupons are usually referred to in terms of the coupon rate (the sum of coupons paid in a year divided by the face value of the bond in question).
Key Features:
- A coupon payment refers to the annual interest paid on a bond between its issue date and the date of maturity.
- The coupon rate is determined by adding the sum of all coupons paid per year, then dividing that total by the face value of the bond.
Origin and History
The origin of the term “coupon” is that bonds were historically issued in the form of bearer certificates. Physical possession of the certificate was (deemed) proof of ownership.
Several coupons, one for each scheduled interest payment, were printed on the certificate. At the date the coupon was due, the owner would detach the coupon and present it for payment (an act called “clipping the coupon”).
The certificate often also contained a document called a talon, which (when the original block of coupons had been used up) could be detached and presented in exchange for a block of further coupons.
How Does a Coupon Bond Work?
Upon the issuance of the bond, a coupon rate on the bond’s face value is specified. The issuer of the bond agrees to make annual or semi-annual interest payments equal to the coupon rate to investors. These payments are made until the bond’s maturity.
Let’s imagine that Apple Inc. issued a new four-year bond with a face value of $100 and an annual coupon rate of 5% of the bond’s face value.
In this case, Apple will pay $5 in annual interest to investors for every bond purchased. After four years, on the bond’s maturity date, Apple will make its last coupon payment. It will also pay the investor back the face value of the bond.
Bond Pricing
Despite the bond’s relatively simple design, its pricing remains a crucial issue. If there is a high probability of default, investors may require a higher rate of return on the bond.
Similar to the pricing of other types of bonds, the price of a coupon bond is determined by the present value formula. The formula is:
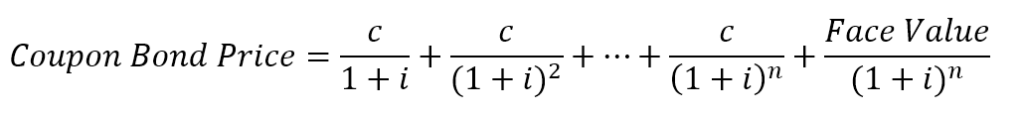
Where:
c = Coupon rate
i = Interest rate
n = number of payments
Also, the slightly modified formula of the present value of an ordinary annuity can be used as a shortcut for the formula above, since the payments on this type of bond are fixed and set over fixed time periods:
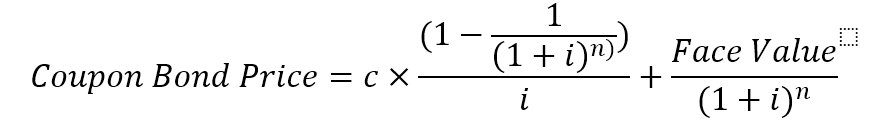
Understanding Coupons
For example, a $1,000 bond with a coupon of 7% pays $70 a year. Typically these interest payments will be semiannual, meaning the investor will receive $35 twice a year.
Because bonds can be traded before they mature, causing their market value to fluctuate, the current yield (often referred to simply as the yield) will usually diverge from the bond’s coupon or nominal yield.
For example, at issue, the $1,000 bond described above yields 7%; that is, its current and nominal yields are both 7%. If the bond later trades for $900, the current yield rises to 7.8% ($70 ÷ $900). The coupon rate, however, does not change, since it is a function of the annual payments and the face value, both of which are constant.
































7 comments on “Bond Coupon in Finance”